等边圆柱体积公式,等边圆柱的体积怎么求?
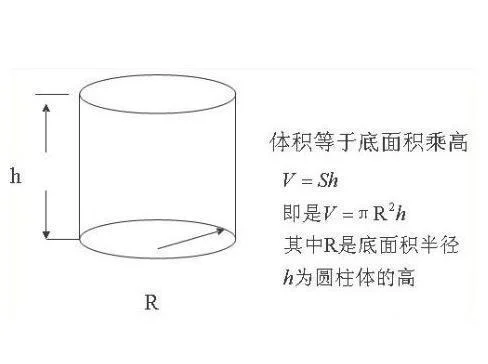
等边圆柱的体积公式是由美国数学家 C. A. Boyd, B. J. Meyer,以及数学家 Harris等人共同发明的,其具体含义是:圆柱和圆锥的投影面积相等。根据这一公式进行计算,可以得到等边圆柱体积公式。这里的图形就是等边圆柱的图形,图中 A和 B是不对称形状,并且通过计算 A、 B和 D三者的体积乘以各自相同比例(即:其中: B为 C点半径2倍; D为 C点半径3倍)得到结论。图中 B和 A、B两个点之间的距离为15 cm,那么其中 C点即为(-6 cm)等边圆柱的体积。
1、等边圆柱的圆锥为三角形,且圆锥半径比等边圆柱的宽。
在等边圆柱空间内,圆的直径与半径相等,故其体积等于圆的直径乘以其尺寸所得的结果之和。由于三角形和圆柱是对称形貌,所以等边圆柱的体积公式也可表示为:其中 A为 C点半径2倍, D为 C点距离 C点数。即:由上式可以证明:等边和圆形之间的距离等于 D=3 (π/d),则等边锥的体积为:由上式还可证明:三角形和圆柱相等时,其体积与两个不同圆锥之间的距离相等。由于等边圆柱不能用对角线或者对中、圆的半径表示圆锥面积,所以必须用三条对角线。
2、求等边圆柱的体积公式:
求等边圆柱的体积公式可将求体积问题转化为几何问题,即用几何学中“点”的概念解决问题。点是图形中具有特殊意义的点,因为它实际上是一组点。点可以是点或一个图形中任何一个面或它与这组“点”或“面”之间的边长关系。点可以是多个角,也可以是任意点。对于求等边圆柱体积问题来说,“点”就是指在等边圆柱与圆锥两个顶点之间具有特殊意义的位置。例如:要求一个长方形 ABC,在已知两点距离(即: A点- B点距离)外还有两个边—— A、 B两点都在 AB上时,就可以通过已知一个三角形 ABD来求 A— B距离(即: A=2倍),然后再通过将两个三角形 ABD之间相隔 a、 b的三角形 ACD与 AB之间相隔β2倍后即可求出其体积公式。
3、求椭圆的体积公式:
例3、求椭圆的厚度,请根据你的需要,选择合适的测量仪器。(1)仪器用途:用于测量椭圆的质量,如椭圆质量、距离等;(2)测量参数:椭圆的直径 x、 y、 z、 h;(3)测量方式:测量时通过调节焦距,使得 z在椭圆中成直角。
4、如图所示和
如图所示,计算了 A、 B和 D三个不同角度的值后,我们就可以得出等边圆柱的体积公式:其中 D为3倍 A半径。其中 B即为(-6 cm)等边圆柱的体积。这里,我们只计算出 C点的体积。通过上述计算可以得到,根据上述原理,只需分别计算出 A、 B和 D三个角度的值即可。如果我们对公式不理解的话,可以直接使用以下公式进行计算。