中位数怎么求公式 | 中位数的简便计算方法
中位数怎么求公式(中位数的简便计算方法)
[ 紅豆blog ] 在应用统计学中平均值、正中间值和众数这三个指标值均能够 用于表明数据信息的集中化发展趋势,集中化发展趋势在应用统计学中就是指一组数据信息向某一中心值看齐的水平,即这种情况数据信息紧紧围绕着哪一个标值遍布。
平均值
平均值即算数平均值,是表明数据信息集中化发展趋势的最普遍指标值,计算方式比较简单,将全部数据信息的标值加总求饶随后除于数据信息的总数量就可以。例如有一组数据信息3,7,6,29,19,31,2,平均值=(3 7 6 29 19 31 2)/7=13.86
中位值
中位值是将数据信息按尺寸排列产生一个数列,取数列正中间部位的数据信息为中位值。假如数据信息的数量为单数,在整列数据信息中中间部位上的数据信息便是中位值。還是以前边那组数据信息3,7,6,29,19,31,2为例子,先依照由小到大的排列顺序,結果为2,3, 6,7, 19, 29, 31,由于数据信息的数量为七个,7恰好处在整列数据信息的第四个也就是中间的部位上,因而中位值为7。
但假如数据信息的数量为双数,那麼在数列的正中间部位上便会有两个数据信息,中位值就相当于这两个数据信息的平均值。例如在前面那组数据信息3,7,6,29,19,31,2的基本上再加11,数据信息的数量就变成八个,排列后为2,3, 6,7, 11,19, 29, 31,7和11处在正中间的部位上,因而中位值=(7 11)/2=9
众数
众数是整组数据信息中出現頻率更大的数据信息,例如每一百个家中所有着的小宠物总数:
狗:69只
猫:45只
锦鲤:22条
小鹦鹉:2只
小兔子:1只
在其中每一百个家中所有着的狗的总数数最多,因而“狗”便是这种情况数据信息中的众数。
再例如,某个品牌鞋店里男皮鞋的市场销售状况以下:
鞋号
销量(双)
24.5
34
25
61
25.5
377
26
210
26.5
119
27
87
25.75
148
由此可见,25.5号鞋的销量较大 ,也就是该数据信息出現的頻率更大。假如测算平均值,那麼均值鞋号为25.75号,销售量平均值为148双,可这两个平均值没啥实际意义,因而立即用25.5号鞋377双的销售量就能直接说清晰真皮皮鞋市场销售的集中化发展趋势,简易又一目了然,不易产生误会。
留意:众数在描述的情况下一直跟分类相关,而不是出現的頻率,例如前边家中小宠物总数的实例中,众数是“狗”,而不是狗的总数即狗做为小宠物在统计分析中出現的頻率69;真皮皮鞋销售量的实例中,“25.5号鞋”是众数,而不是25.5号鞋的销售量377,377也是25.5号鞋在统计分析中出現的頻率。
一组数据信息中能够 有众数,还可以沒有众数,这一点与平均值和中位值不一样,一切一组数据信息毫无疑问会出现平均值与中位值。例如最前边那组数据信息3,7,6,29,19,31,2中,各数据信息出現的頻率是一致的,因而沒有众数;假如将在其中的7换成6 ,这种情况数据信息就变成3,6,6,29,19,31,2,由此可见6出現了2次,而别的标值均只出現一次,因而6就变成这种情况数据信息中的众数。
中位值和众数大部分不会受到极端化值的危害,但平均值受极端化值的危害非常大,例如最前边那组数据信息3,7,6,29,19,31,2的平均值为13.86,假如将31换成299,那麼平均值=(3 7 6 29 19 299 2)/7=52.14,但这种情况数据信息的中位值仍是7。
由此可见,假如一组数据信息中带有极端化值,用中位值来叙述这种情况数据信息的集中化遍布发展趋势是再适合但是的。例如,在统计分析英国家庭年收入状况时,最常见的方式 便是看一下英国家庭年收入中位值的状况,由于如果是测算家庭年收入平均值,非常容易被占人口数量不大的高收益家中所影响,例如比尔.盖茨和扎克伯格等。
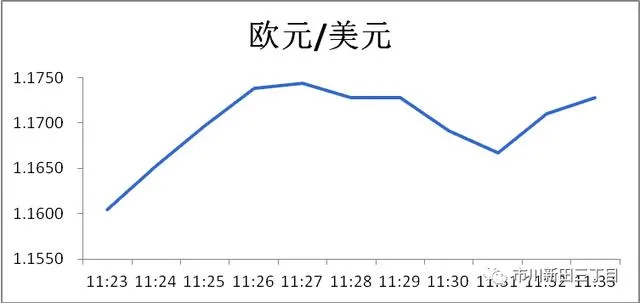
以某股票交易时间11:23至11:33期内欧/美金的市场报价为例子,假定每分价格一次,在这段时间现有11个价格,利率的平均值为1.1699,中位值为1.1710,1.1728的价格出現三次,因而期内利率的众数为1.1728
时间
欧/美金
平均值
低高排列
中位值
众数
11:23
1.1604
1.1699
11:23
1.1604
11:24
1.1653
11:24
1.1653
11:25
1.1697
11:31
1.1667
11:26
1.1738
11:30
1.1692
11:27
1.1744
11:25
1.1697
11:28
1.1728
11:32
1.1710
1.1710
11:29
1.1728
11:28
1.1728
1.1728
> 11:30
1.1692
11:29
1.1728
11:31
1.1667
11:33
1.1728
11:32
1.1710
11:26
1.1738
11:33
1.1728
11:27
1.1744
价格走势图表为
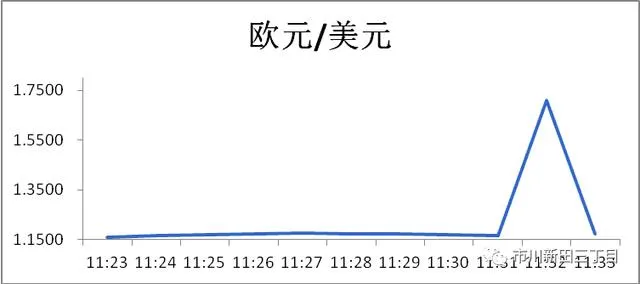
在外汇交易市场中常常会产生价格错误的状况,也就是系统软件价格比较严重偏移销售市场一切正常的起伏范畴,假定11:33系统软件将本属一切正常的1.1710不正确地报成1.7110,那麼能够 见到利率的平均值会从1.1699变为1.2190,中位值从1.1710变为1.1728,而利率的众数仍为1.1728,由此可见平均值受极端化不正确价格的危害有多大,而中位值和众数主要表现基础平稳。
时间
欧/美金
平均值
低高排列
中位值
众数
11:23
1.1604
1.2190
11:23
1.1604
11:24
1.1653
11:24
1.1653
11:25
1.1697
11:31
1.1667
11:26
1.1738
11:30
1.1692
11:27
1.1744
11:25
1.1697
11:28
1.1728
11:28
1.1728
1.1728
11:29
1.1728
11:29
1.1728
1.1728
11:30
1.1692
11:33
1.1728
11:31
1.1667
11:26
1.1738
11:32
1.7110
11:27
1.1744
11:33
1.1728
11:32
1.7110
价格走势图表上不正确价格比较严重偏移一切正常起伏区段。
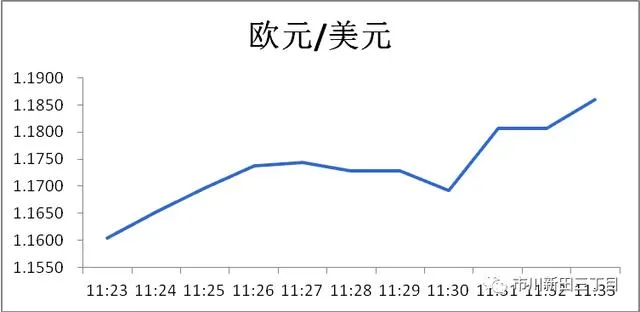
但有的状况下,利率尽管与前一个价格相差甚远,并不是因为出错价,只是销售市场利率自身的确发生了大的起伏,例如重特大经济数据发布后常常会看到利率忽然提升某一重要压力位,随后一路上行,这类状况下,在利率平均值随着起伏的另外,利率的中位值将会变化并不大,但众数会产生大的转变,乃至有双众数的状况产生。
时间
欧/美金
平均值
低高排列
中位值
众数
11:23
1.1604
1.1733
11:23
1.1604
11:24
1.1653
11:24
1.1653
11:25
1.1697
11:30
1.1692
11:26
1.1738
11:25
1.1697
11:27
1.1744
11:28
1.1728
1.1728
11:28
1.1728
11:29
1.1728
1.1728
11:29
1.1728
11:26
1.1738
11:30
1.1692
11:27
1.1744
11:31
1.1807
11:31
1.1807
1.1807
11:32
1.1807
11:32
1.1807
11:33
1.1860
11:33
1.1860
总结:
-
平均值、正中间值和众数这三个指标值均能够 用于表明数据信息的集中化发展趋势;
-
平均值的测算非常简单,但数列中一切一个值的转变对平均值均有影响,因而非常容易遭受极端化标值的影响;
-
在预估中位值以前,必须先向数据信息按尺寸开展排序,随后选择正中间的标值,假如数据信息数量为双数,中位值则为正中间2个数据信息的算数平均值;
-
中位值较为适用数列中带有极端化值的状况;
-
一切一组数据信息,无论数据信息的文件格式是双数還是单数,一定有平均值与中位值;
-
众数与出現的頻率相关;
-
一组数据信息中能够 有众数,乃至是双众数,还可以沒有众数;
-
众数一直跟分类相关,而不是出現的頻率;
-
在对极端化数据信息的比较敏感度层面,正中间值<众数<平均值。