直角三角形面积公式(直角三角形怎么算平方)
这道题是2000年AMC 10第19题(也是AMC 12第21题)。

从直角三角形的斜边上的某一个点,画两条直角边的平行线,将该直角三角形分成三部分:一个正方形和两个小的直角三角形。这两个小直角三角形中的一个的面积,是正方形面积的m倍,求另一个小直角三角形的面积与正方形面积之比。
既然是求小三角形的面积与正方形面积之比,不妨设正方形的面积为1,即正方形的边长也为1;则已知的那个小三角形的面积为m。如下图所示:

在图中,右下角小三角形的面积为m,其中一条直角边为1,故另一条直角边(大三角形直角边的一部分)为2m。设另一个小三角形的未知直角边为x。
这样,两个小三角形的斜边长度分别为root( 4m^2+1)和root( x^2+1)。对大三角形而言,根据勾股定理,有:
(2m+1)^2 + (x+1)^2 = (root( 4m^2+1)+ root( x^2+1)) ^2
化简得到:
4m^2 x^2 – 4mx +1=0
即:(2mx – 1) = 0
x= 1/ (2m)
故另一个小三角形的面积为:1/(4m),为正方形面积的1/(4m)。
还有更简单的方法可以快速求出m。容易发现,两个小三角形是相似三角形!(之前讲过!)故其对应边的比例相等,即:
x :1 = 1 :2m
即x= 1/ (2m),同样可以得到结果。
是不是更清爽?
相关内容
-
昆虫备忘录仿写400字
昆虫备忘录仿写400字,,昆虫备忘录仿写可爱的小狗:我家有一只小狗,它长着圆圆的头,小小的耳朵,圆溜溜的黑眼睛,像两颗明亮的小玻璃球。黑黑的小鼻子真像一个三角形,嘴巴里长着尖尖牙齿,短短的小尾巴一摇一摆,它的毛黄黄的,真是越看越可爱!有时,我忍不住要俯身去摸它那又软又滑的毛,可乖了......可爱的小狗我家有一只小狗,它长着圆圆的头,小小的耳朵,圆溜溜的黑眼睛,像两颗明亮的小玻璃球。黑黑的小鼻子真...
-
千岛湖在哪里个城市?千岛湖旅游攻略,一起
千岛湖在哪里个城市?千岛湖旅游攻略,一起来了解一下,,千岛湖是世界上最大的淡水湖,是国家级风景名胜区。景区面积480平方公里,水域面积384平方公里,共有大小岛屿3300多个。千岛湖的美,不仅仅在于湖光山色和瀑布溪流,还在于它的山水文化背景。著名文学家鲁迅先生在他的狂人日记中这样写道:“如果有人问我怎样能够写出这么优美的文字来,我一定会告诉他:千岛湖!”1、千岛湖的湖名千岛湖原名杭州湾水库,相传宋...
-
卡塔尔面积和青岛差不多(“中国队”却瓜
卡塔尔面积和青岛差不多(“中国队”却瓜分了二千多亿),,青岛日报社/观海新闻11月21日讯 举世瞩目的卡塔尔世界杯已盛装启幕。在微博上,由央视新闻创建的话题“卡塔尔面积和青岛差不多”突然火了,成为热搜。微博截图数据表明,卡塔尔的国土面积为11521平方公里,而青岛的区域总面积为11293平方公里,卡塔尔的面积约比青岛大2%,二者的面积的确差不多。央视新闻在微博中写到:①卡塔尔面积和青岛差不多,是目...
-
怎么看秋田犬品相(什么样的秋田犬品相好)
怎么看秋田犬品相(什么样的秋田犬品相好),,挑选秋田犬要从外貌、身形、躯干、毛发这四个方面来判断,当然自己当宠物养的话,其实对自己眼缘还是最重要的。秋田犬的外貌从秋田犬的样貌外形来看,整体外貌给人感觉威风凛凛,高大威猛,有气势,头部呈现三角形,两只耳朵保持直立的状态,与后颈保持在同一直线上。同时,从正面来看,尾巴要又大又密实,看起来与宽阔的头部是相呼应的。秋田犬的身形头部大小与身体比例是协调一致的...
-
a3大还是a4大,a3大还是4K大
a3大还是a4大,a3大还是4K大,,1、A3纸指的是国际通用标准A3规格的纸张,其大小为297毫米*420毫米,A4纸的尺寸是210毫米×29 7毫米。A3纸是A4纸的2倍。2、按照纸张幅面的基本面积,把幅面规格分为A系列、B系列和C系列,幅面规格为A0的幅面尺寸为841毫米×1189毫米,幅面面积为1平方米;B0的幅面尺寸为1000毫米×1414毫米,幅面面积为1.5平方米;C0的幅面尺寸为9...
-
千岛湖在哪里个城市?千岛湖旅游攻略,一起
千岛湖在哪里个城市?千岛湖旅游攻略,一起来了解一下,,千岛湖是世界上最大的淡水湖,是国家级风景名胜区。景区面积480平方公里,水域面积384平方公里,共有大小岛屿3300多个。千岛湖的美,不仅仅在于湖光山色和瀑布溪流,还在于它的山水文化背景。著名文学家鲁迅先生在他的狂人日记中这样写道:“如果有人问我怎样能够写出这么优美的文字来,我一定会告诉他:千岛湖!”1、千岛湖的湖名千岛湖原名杭州湾水库,相传宋...
-
excel输入开根号,如何快速找到需要的公式
excel输入开根号,如何快速找到需要的公式?,,一、什么是单元格中的开立方数在Excel中,如果使用函数F3=SUM(A1,B1),那么我们就可以通过一个简单的运算来得到这个值。例如:1、计算下面两个数的和为多少? 2、求下列各组数值之和是多少?这两个问题都是要求出两列数据的和的绝对值的。二、怎么输入开平方数方法一打开需要计算的表格后点击【插入】-【行】,然后选择【单选按钮】。接着再点下面的下拉...
-
在戴尔电脑 wo rd中插入数学公式
在戴尔电脑 wo rd中插入数学公式,,要在电脑 word中插入数学公式,是一件很困难的事情。比如在电脑 Word中我们不可能把一个公式在不同的软件中进行识别,因此必须使用到 Excel来完成。那么我们如何才能将公式和操作转换为所需要的格式呢?本文就将教你如何利用 Excel,对自己的 word文件进行编辑的计算过程。1、打开文档打开 Word文档,我们需要先打开 word,然后才能编辑数学过程。...
-
苦瓜焖排骨简单好吃的做法(苦瓜炖排骨怎
苦瓜焖排骨简单好吃的做法(苦瓜炖排骨怎么做好吃窍门),, 苦瓜又叫凉瓜,搭配排骨焖煮,吃起来美味,而且还具有清热去火,解暑祛痱,排毒养颜的功效。下面献上小编整理的苦瓜焖排骨做法,相信一定会对大家有所帮助。苦瓜焖排骨食材清单苦瓜焖排骨的制作步骤1.准备所需材料,排骨剁成小块。(排骨买回来就已经剁好了)2.苦瓜洗净,对半切开,用小勺挖出里面的瓜嚢。3.再切成三角形。4.蒜和姜切成片。5.将排骨洗净,...
-
柯基如何辨别(为什么柯基不能打)
柯基如何辨别(为什么柯基不能打),,在挑选柯基幼犬前,与它进行互动,观察柯基幼犬精神状态,精神涣散的幼犬多为病犬;从正面看以柯基的鼻子为一点,柯基两个耳朵尖为两点,这三点组成一个三角形;柯基幼犬步态自如流畅,四肢矮短,骨骼粗壮。 柯基如何辨别?在挑选柯基幼犬前,与它进行互动,观察柯基幼犬精神状态,精神涣散的幼犬多为病犬;从正面看以柯基的鼻子为一点,柯基两个耳朵尖为两点,这三点组成一个三角形;柯基...
-
鸡蛋摊饼的做法 面糊,摊鸡蛋饼面糊怎么调
鸡蛋摊饼的做法 面糊,摊鸡蛋饼面糊怎么调,,1、准备面粉、鸡蛋、花椒粉、盐、葱花,全部倒入碗中搅拌均匀。2、锅中倒入食用油,刷匀,倒入面糊。3、煎至两面金黄,即可出锅,切成三角形,装盘即可。...
-
secx等于什么,secx等于什么图像
secx等于什么,secx等于什么图像,,1、secx是正割函数,为直角三角形斜边与某个锐角的邻zd边的比,在数值上等于余弦函数的倒数。正割指的是直角三角形,斜边与某个锐角的邻边的比,叫做该锐角的正割,用 sec(角)表示。2、正割函数的性质有:定义域,x不能取90度,内270度,负90度,负270度等值;即为容{x|x≠kπ+π/2,k∈Z}。值域,secx≥1或secx≤-1。y=secx是偶...
-
金毛食量计算公式(金毛犬食量)
金毛食量计算公式(金毛犬食量),,金毛食量计算公式:假定一只金毛体重33kg,将体重(kg)X3次=35937,再将1的答案开根(=18957),再将2的答案开根号(=1376),将3的答案÷125(=1720)得出这条金毛一天需要的卡路里为1720卡路里。金毛食量计算公式假定:一岁的金毛犬,体重33公斤,那么金毛狗狗一天需要的卡路里这样计算:1.将狗的体重(kg)乘以3次(33x33x33=35...
-
世界哪个国家面积最大?不是俄罗斯也不是美
世界哪个国家面积最大?不是俄罗斯也不是美国,而是这个袖珍国,,面积最大的国家是哪个?答案当然是俄罗斯,因为俄罗斯领土总面积为1130万平方公里,约占世界陆地总面积的五分之一。那么世界哪个国家的面积最大呢?答案就是加拿大,其陆地总面积为5240万平方公里,其中加拿大土地面积为3560万平方公里。如果按照地理位置划分的话,加拿大领土主要分布在北美大陆上,包括阿尔伯塔省、萨斯喀彻温省、安大略省、魁北克省...
-
大面积种植的草花发芽后怎么养护(四个方面
大面积种植的草花发芽后怎么养护(四个方面要知道),,草花是十分喜光的,在它生长的前期还会有一些杂草长出。但由于种植面积很大,草花也是十分繁忙的。就算是养花新手们,也不想错过这一段养花卉的时光。那么草花的大面积栽种后要怎样养呢?该怎么养护呢?一起来看看吧!一、怎么养?草花喜欢温暖的环境,在它生长的过程中是需要有充足的阳光照射的。所以一定要注意它在养护过程中的温度,如果温度过低就会导致其生长缓慢,或者...
-
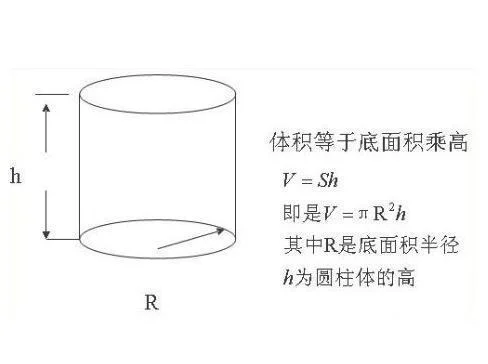
等边圆柱体积公式,等边圆柱的体积怎么求?
等边圆柱体积公式,等边圆柱的体积怎么求?,,等边圆柱的体积公式是由美国数学家 C. A. Boyd, B. J. Meyer,以及数学家 Harris等人共同发明的,其具体含义是:圆柱和圆锥的投影面积相等。根据这一公式进行计算,可以得到等边圆柱体积公式。这里的图形就是等边圆柱的图形,图中 A和 B是不对称形状,并且通过计算 A、 B和 D三者的体积乘以各自相同比例(即:其中: B为 C点半径2倍;...
-
股票软件如何设置公式(指标安装步骤)
股票软件如何设置公式(指标安装步骤),,对新入市的散户来说,经过一段时间买卖股票,以及朋友说的炒股公式选股多么的牛,选出的股票大涨,听了之后心痒痒,也想自己也能写选出牛股的公式,在这里给这些朋友介绍下通达信股票软件编写公式的方法通达信股票软件如何编写股票软件的选股公式通达信股票软件首先打开股票软件,点击登录点击上面的菜单的系统,下拉树中选择公式系统的公式管理器按钮点击公式管理器后,进入公式管理器界...
-
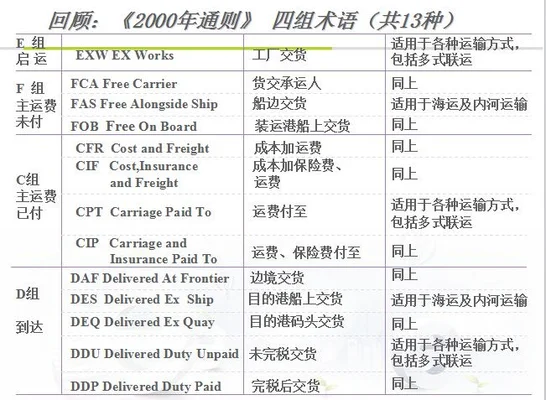
出口fob价格计算公式:FOB(离岸价)÷运距×
出口fob价格计算公式:FOB(离岸价)÷运距×保险费率,,在出口 fob中,由于其对国际结算要求,不同, fob的计算方式也不同。所以在计算 fob价格时一定要注意各种因素。不能只看价格公式,否则就不是专业人士了,也不能很好的为大家解答。今天介绍一下 Fob出口价格计算公式。其实这是一种很简单的计算方法,但如果要说是非常准确的话,那是比较困难的。因为很多的 Fob在出口的时候是有很多因素的,其中...